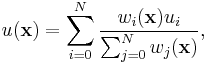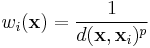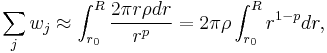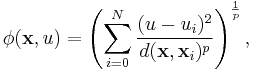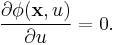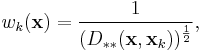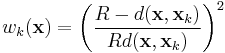Inverse distance weighting
Inverse distance weighting (IDW) is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points. Here, the value at the unknown point is a weighted sum of the values of N known points.
Contents |
Shepard's method
A general form of finding an interpolated value u at a given point x based on samples 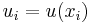 for
for 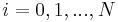 using IDW is an interpolating function:
using IDW is an interpolating function:
where
is a simple IDW weighting function, as defined by Shepard,[1] x denotes an interpolated (arbitrary) point, xi is an interpolating (known) point,  is a given distance (metric operator) from the known point xi to the unknown point x, N is the total number of known points used in interpolation and
is a given distance (metric operator) from the known point xi to the unknown point x, N is the total number of known points used in interpolation and  is a positive real number, called the power parameter.
is a positive real number, called the power parameter.
Here weight decreases as distance increases from the interpolated points. Greater values of  assign greater influence to values closest to the interpolated point. For 0 < p < 1 u(x) has smooth peaks over the interpolated points xi, while as p > 1 the peaks become sharp. The choice of value for p is therefore a function of the degree of smoothing desired in the interpolation, the density and distribution of samples being interpolated, and the maximum distance over which an individual sample is allowed to influence the surrounding ones. For two dimensions, power parameters
assign greater influence to values closest to the interpolated point. For 0 < p < 1 u(x) has smooth peaks over the interpolated points xi, while as p > 1 the peaks become sharp. The choice of value for p is therefore a function of the degree of smoothing desired in the interpolation, the density and distribution of samples being interpolated, and the maximum distance over which an individual sample is allowed to influence the surrounding ones. For two dimensions, power parameters 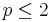 , cause the interpolated values to be dominated by points far away, since with a density
, cause the interpolated values to be dominated by points far away, since with a density  of data points and neighboring points between distances
of data points and neighboring points between distances 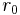 to
to  , the summed weight is approximately
, the summed weight is approximately
which diverges for 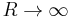 and
and 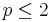 . For N dimensions, the same argument holds for
. For N dimensions, the same argument holds for 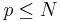 .
.
Shepard's method is a consequence of minimization of a functional related to a measure of deviations between tuples of interpolating points {x, u} and i tuples of interpolated points {xi, ui}, defined as:
derived from the minimizing condition:
The method can easily be extended to higher dimensional space and it is in fact a generalization of Lagrange approximation into a multidimensional spaces. A modified version of the algorithm designed for trivariate interpolation was developed by Robert J. Renka and is available in Netlib as algorithm 661 in the toms library.
Lukaszyk-Karmowski metric
Yet another modification of the Shepard's method was proposed by Łukaszyk[2] also in applications to experimental mechanics. The proposed weighting function had the form:
where 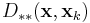 is the Lukaszyk-Karmowski metric chosen also with regard to the statistical error probability distributions of measurement of the interpolated points.
is the Lukaszyk-Karmowski metric chosen also with regard to the statistical error probability distributions of measurement of the interpolated points.
Modified Shepard's Method
Another modification of Shepard's method calculates interpolated value using only nearest neighbors within R-sphere (instead of full sample). Weights are slightly modified in this case:
When combined with fast spatial search structure (like kd-tree) it becomes efficient N*logN interpolation method suitable for large-scale problems.
References
- ^ Shepard, Donald (1968). "A two-dimensional interpolation function for irregularly-spaced data". Proceedings of the 1968 ACM National Conference. pp. 517–524. doi:10.1145/800186.810616.
- ^ *A new concept of probability metric and its applications in approximation of scattered data sets